Tercero BGU, Matemática.

Buenas tardes estudiantes.

Deber:  Realice la actividad 5 de la página 20. 

Resolviendo ecuaciones exponenciales y logarítmicas

Objetivos de aprendizaje

·         Resolver ecuaciones exponenciales.

·         Resolver ecuaciones logarítmicas.

Introducción

Como sabes, a veces el álgebra requiere que resuelvas ecuaciones para encontrar valores desconocidos. Esto también sucede con las ecuaciones exponenciales y logarítmicas. Hay algunas estrategias, junto con algunas propiedades, que puedes usar para resolver estas ecuaciones.

Resolviendo ecuaciones exponenciales

Puedes ver una ecuación como 4^x = 16 y la resuelves preguntándote, “¿4 a qué potencia es 16? 4² es 16, entonces x = 2.” Ecuaciones como 4^x = 17 son un poco más difíciles. Sabes que x debe ser un poco más de 2, porque 17 es un poco más que 16. Una manera de encontrar x con más precisión, es usando logaritmos.

Cuando resolvías otras ecuaciones algebraicas, normalmente te basabas en la idea de que puedes cambiar ambos lados de la ecuación de la misa manera y obtener una ecuación válida. Esto también sucede con los logaritmos: Si x = y, entonces log_bx = log_by, no importa qué sea b.

Veamos esto con una ecuación cuya solución ya conozcas: 4^x = 16. Puedes usar logaritmo común (logaritmo común) o logaritmo natural (logaritmo natural). En el siguiente ejemplo, usarás log común.

Ejemplo
Problema	Resolver 4x = 16.
	4x = 16 log 4x = log 16	Saca el logaritmo común de ambos lados. (Recuerda, cuando la base no está escrita, se trata de la base 10.) ¿Qué puedes hacer con la nueva ecuación?
	log 4x = log 16 x log 4 = log 16	Usa la propiedad de la potencia de los logaritmos para simplificar el logaritmo del lado izquierdo de la ecuación.
	x log 4 = log 16	Recuerda que log 4 es un número. Puedes dividir ambos lados de la ecuación entre log 4 para obtener x.
Respuesta		Usa una calculadora para evaluar los logaritmos y el cociente.

Ya sabías, x = 2. Ahora intentemos con nuestro ejemplo más difícil, 4^x = 17. El procedimiento es exactamente el mismo.

Ejemplo
Problema	Resolver 4x = 17.
	4x = 17 log 4x = log 17	Saca el logaritmo común de ambos lados.
	log 4x = log 17 x log 4 = log 17	Usa la propiedad de la potencia de los logaritmos para simplificar el logaritmo del lado izquierdo.
	x log 4 = log 17	Divide ambos lados entre log 4 para obtener x
Respuesta		Usa una calculadora para evaluar los logaritmos y el cociente.

Pudiste haber usado el log común o el log natural con el mismo ejemplo. Usaste una de estas bases, para poder usar la calculadora y encontrar los valores.

Ejemplo
Problema	Resolver e2x = 54.
	e2x = 54 ln e2x = ln 54	Como la base es e, usa el logaritmo natural. (Si la base fuera 10, usarías el logaritmo común.)
	ln e2x = ln 54 2x = ln 54	Recuerda que los logaritmos y las funciones exponenciales son inversos. Cuando tienes logbbm, el logaritmo deshace el exponente y el resultado es sólo m. Entonces ln e2x = logee2x = 2x.
	x =	Divide ambos lados entre 2 para obtener x.
Respuesta	x = 1.99449...	¡Usa una calculadora para evaluar los logaritmos y el cociente en la derecha y ya terminaste!

Otro tipo de ecuación exponencial tiene expresiones exponenciales a ambos lados. Cuando las bases son las mismas o los exponentes son los mismos, puedes simplemente comparar las partes que son diferentes. Veamos estos ejemplos.

Ejemplo
Problema	Resolver 32x + 5 = 33x – 2.
	32x + 5 = 33x – 2	Aquí hay dos expresiones exponenciales con la misma base. Si las dos expresiones son iguales, entonces sus exponentes deben ser iguales. (Piensa en ello — si tienes 3a y 3b y a ≠ b, entonces 3a no puede tener el mismo valor que 3b.)
	2x + 5 = 3x – 2	Entonces, escribe una nueva ecuación que iguale los exponentes uno con otro.
	5 = x – 2 7 = x	Resuelve la ecuación lineal como lo haces normalmente.
Comprobación	32(7) + 5 = 33(7) – 2 319 = 319	Comprueba la solución en la ecuación original. No necesitas calcular 319. ¡Cuando ambos lados sean iguales, sabes que es correcto!
Respuesta	x = 7

Ejemplo
Problema	Resolver (x + 4)8 = 78.
	(x + 4)8 = 78	De nuevo. Tienes dos expresiones exponenciales que son iguales una con otra. En este caso, ambos lados tienen el mismo exponente y esto significa que las bases deben ser iguales.
	x + 4 = 7	Escribe una nueva ecuación que iguale las bases una con otra.
	x = 3	Resuelve la ecuación lineal como lo haces normalmente.
Comprobación	(3 + 4)8 = 78 78 = 78	Comprueba la solución en la ecuación original. No necesitas calcular 78. ¡Cuando ambos lados sean iguales, sabes que es correcto!
Respuesta	x = 3

Resolver 103x – 2 = 13. A) x = 5 B) x = 1.03798… C) x = 1.52164… D) x = 3.11394… Mostrar/Ocultar Respuesta

Resolviendo ecuaciones logarítmicas

Hay varias estrategias que puedes usar para resolver ecuaciones logarítmicas. La primera ya la has usado antes: ¡Reescribir la ecuación logarítmica como una ecuación exponencial!

Ejemplo
Problema	Resolver ln x = 4.657. Con x en milésimas.
	ln x = 4.657 loge x = 4.657 e4.657 = x	Recuerda que los logaritmos naturales tienen base e. Reescribe este logaritmo como una ecuación exponencial.
Respuesta	105.3196… = x x ≈ 105.320	Usa una calculadora para evaluar e4.657 y redondea a milésimas.

Esto funciona sin importar la base.

Ejemplo
Problema	Resolver log7 x = 3.843. Con x en milésimas.
	log7 x = 3.843 73.843 = x	Reescribe este logaritmo como una ecuación exponencial.
Respuesta	1768.9345…= x x ≈ 1768.935	Usa una calculadora para evalúa 73.843y redondea a milésimas.

Las ecuaciones logarítmicas pueden tener entradas donde la variable tiene un coeficiente distinto de 1. O donde la variable está al cuadrado. En estos casos, necesitas completar algunos pasos para resolver la variable.

Ejemplo
Problema	Resolver log53x2 = 1.96. Con x en centésimas.
	51.96 = 3x2	Reescribe este logaritmo como una ecuación exponencial.
	23.44127… = 3x2	Evalúa 51.96.
	7.81375… = x2 x = ±2.7953… x ≈ ±2.80	Resuelve como normalmente lo harías. En este caso, divide ambos lados entre 3, luego usa la propiedad de la raíz cuadrada para encontrar los posibles valores de x. No olvides que cuando usas la propiedad de la raíz cuadrada, debes considerar las raíces positiva y negativa. Redondea a centésimas.
Comprobación	log5 3x2 = 1.96 log5 3(-2.80)2 = 1.96 log5 3(7.84) = 1.96 log5 23.52 = 1.96	Comprueba tu respuesta sustituyendo el valor de x en la ecuación original. Como (-2.80)2 y (+2.80)2 son positivos no necesitamos comprobar +2.80 separadamente.
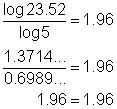		Aplica la fórmula de cambio de base para cambiar de base 5 a base 10. La comprobación muestra que tomando en cuenta el redondeo, resulta un enunciado válido, por lo que sabes que la respuesta es correcta.
Respuesta	x ≈ ±2.80

Las ecuaciones podrían también incluir más de un logaritmo. Puedes usar las propiedades de los logaritmos para combinarlos en un sólo logaritmo. Nota: Encontrarás útil tomar nota de las propiedades que usas en cada paso, para asegurarte que las estás usando apropiadamente y para encontrar errores.

Ejemplo
Problema		Resolver .
			Primero observa que todos los logaritmos tienen la misma base. (Estos son logaritmos comunes, por lo que todas las bases son 10). Cuando usas las propiedades, es absolutamente necesario que todas las bases sean iguales.
			Usa la propiedad de la potencia para reescribir 2log 3 como log 32 y para reescribir  como .
	log 9 + log 4 – log 3 = log x		Evalúa los exponentes.
	log (9 • 4) – log 3 = log x log 36 – log 3 = log x		Usa la propiedad del producto, , para combinar log 9 + log 4.
	log  = log x log 12 = log x		Usa la propiedad del cociente, , para combinar log 36 – log 3.
Respuesta	x = 12		Como el logaritmo de 12 y el logaritmo de x son iguales, xdebe ser igual a 12.