Segundo BGU, Física.

Buenas tardes estudiantes.

Deber: Realizar el ejercicio 6 de las páginas 54 y 55, literales  47, 50, 55 y 62.

Movimiento rectilíneo uniformemente acelerado en mecánica newtoniana[editar]

En mecánica clásica el movimiento rectilíneo uniformemente acelerado (MRUA) presenta dos características fundamentales:

1. La trayectoria es rectilínea
2. La aceleración sobre la partícula son constantes.

sabiendo que:

${\displaystyle \mathbf {F} =m\,\mathbf {a} }$

Dado que la masa es una constante, la aceleración constante tiene como causa una fuerza resultante constante.

Por lo tanto, esto determina que:

1. La velocidad varía linealmente respecto del tiempo.
2. La posición varía según una relación cuadrática respecto del tiempo.

La figura muestra las relaciones de la aceleración, la velocidad y el espacio respecto del tiempo, aceleración (constante, recta horizontal), velocidad (recta con pendiente) y del desplazamiento (parábola).

La aceleración a constante, en el ejemplo:

${\displaystyle a=a_{0}}$

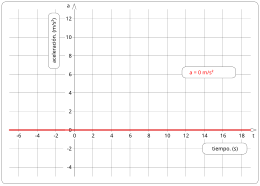podemos ver la gráfica de la función de la aceleración respecto al tiempo, se ve claramente que son rectas horizontales.

La velocidad v para un instante t dado es:

${\displaystyle v(t)=at+v_{0}\,}$

Para una misma velocidad inicial con distintas aceleraciones tenemos un haz de rectas de distinta pendiente:

con una misma aceleración y distintas velocidades iniciales tenemos rectas paralelas como las de los graficos:

Finalmente el espacio e en función del tiempo se expresa por:

${\displaystyle e(t)={\frac {1}{2}}at^{2}+v_{0}t+e_{0}}$

donde ${\displaystyle e_{0}\,}$ es la posición inicial.

La función del espacio respecto al tiempo, con una aceleración constante y distinta de cero, es una parabola, la velocidad inicial y la posición inicial son fijos, para distintas aceleraciones tenemos distintas parabolas, que pasan por el mismo punto de la posición inicial y en ese punto presentan la misma pendiente.

Con una misma aceleración y con la misma posición inicial, pero con distintas velocidades iniciales las gráficas son de esta forma:

La gráfica en el caso de una misma aceleración y misma velocidad inicial, pero con distintas posiciones iniciales, las gráficas serian de esta forma:

Además de las relaciones básicas anteriores, existe una ecuación que relaciona entre sí el desplazamiento y la rapidez del móvil. Ésta se obtiene despejando el tiempo de (2a) y sustituyendo el resultado en (3):

${\displaystyle v^{2}=2a(e-e_{0})+v_{0}^{2}\,}$

Deducción de la velocidad en función del tiempo[editar]

Se parte de la definición de aceleración

${\displaystyle {\cfrac {dv}{dt}}=a}$

y se integra esta ecuación diferencial lineal de primer orden

${\displaystyle \int _{v_{0}}^{v}dv=\int _{t_{0}}^{t}a\,dt}$

se resuelve la integral

${\displaystyle v=a(t-t_{0})+v_{0}\ }$

donde ${\displaystyle v_{0}\,}$ es la velocidad del móvil en el instante inicial ${\displaystyle t_{0}\,}$.

En el caso de que el instante inicial sea ${\displaystyle t_{0}=0\,}$, será

${\displaystyle v=at+v_{0}\ }$

Deducción de la posición en función del tiempo[editar]

A partir de la definición de velocidad

${\displaystyle {\cfrac {de}{dt}}=v}$

integrando

${\displaystyle \int _{e_{0}}^{e}de=\int _{t_{0}}^{t}v\,dt}$

en la que se sustituye el valor obtenido anteriormente para ${\displaystyle v=v(t)\,}$

${\displaystyle \int _{e_{0}}^{e}de=\int _{t_{0}}^{t}[a(t-t_{0})+v_{0}]dt}$

resolviendo la integral, y teniendo en cuenta que ${\displaystyle a\,}$ y ${\displaystyle v_{0}\,}$ son constantes:

${\displaystyle e={\frac {1}{2}}a(t-t_{0})^{2}+v_{0}(t-t_{0})+e_{0}}$

donde ${\displaystyle e_{0}\,}$ la posición del móvil en el instante ${\displaystyle t_{0}\,}$.

En el caso de que en el tiempo inicial sea ${\displaystyle t_{0}=0\,}$ la ecuación sería:

${\displaystyle e={\frac {1}{2}}at^{2}+v_{0}t+e_{0}}$