Tercero matemática.

Buenas tardes estudiantes.

Deber: Lea, analice y subraye las ideas principales y secundarias en el libro, además realice un mapa conceptual de las paginas expuestas con sus respectivas gráficas, en hojas de papel ministro, OBSERVAR Y ANALIZAR LOS EJERCICIOS RESUELTOS EN LAS PAGINAS PLANTEADAS.
ACTIVIDADES A REALIZAR: (Pág.: 155 todos)

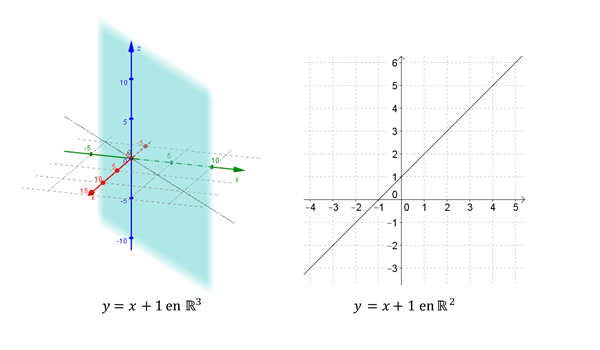
Pero ¿qué representa esta ecuación en $R^3$? En $R^3$ es un plano paralelo al eje $z$, y en $R^2$ es una recta:

Para definir un plano es suficiente conocer un vector perpendicular al plano y un punto del mismo. ¿Qué datos permiten definir una recta en $R^3$?

Para definir en forma vectorial una recta en $R^3$, es suficiente conocer un punto de la recta y un vector director que indique la dirección de la misma, o sea un vector paralelo a la recta.

Ecuación vectorial de la recta

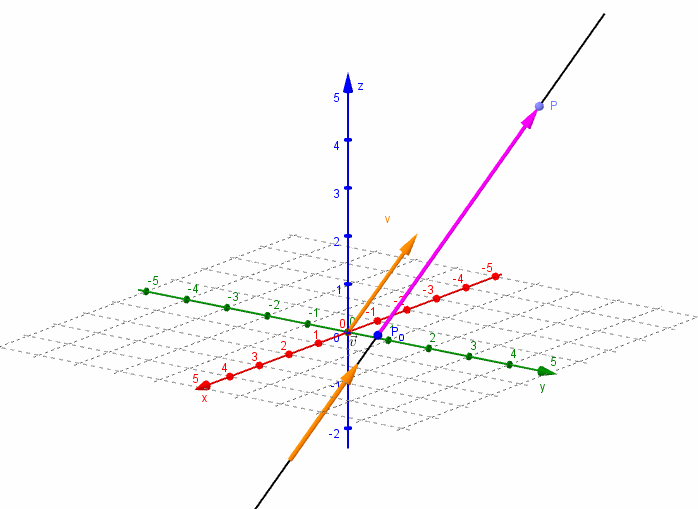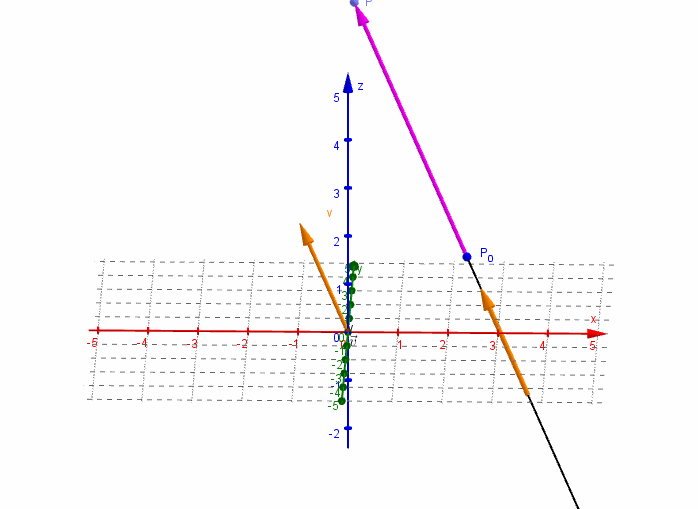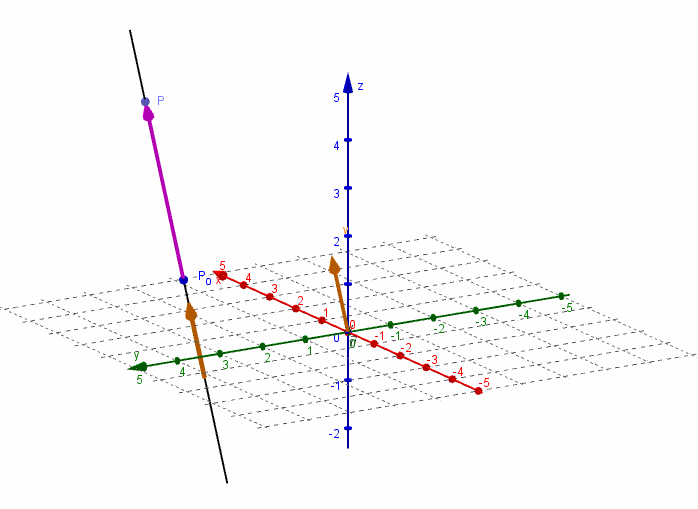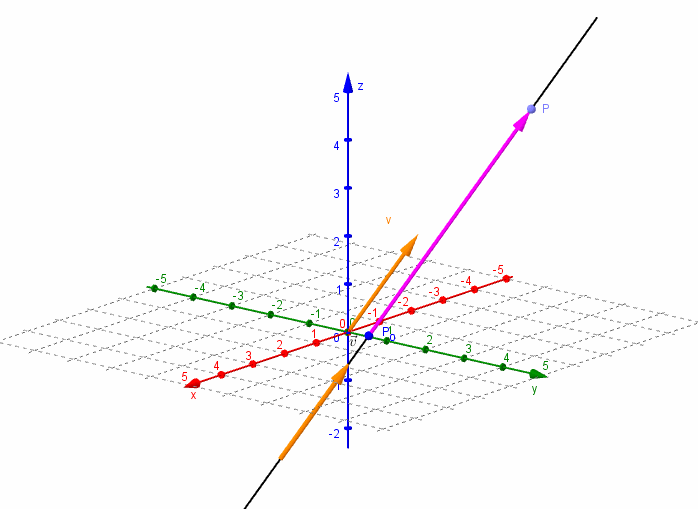
Dados un vector $\vec{v}=\left(v_1,v_2,v_3\right)$ y un punto $P_0\left(x_0,y_0,z_0\right)$, nos proponemos hallar la ecuación de la recta $r$ que pasa por el punto $P_0$ y es paralela al vector $\vec{v}$.

Consideremos un punto $P\left(x,y,z\right)$ perteneciente a la recta r. El vector $\overrightarrow{P_{0}P}$ resultará paralelo al vector director $\vec{v}$:

$$\overrightarrow{P_{0}P}=\alpha \vec{v}$$

$$\left(x–x_0,y–y_0,z–z_0\right)=\alpha \left(v_1,v_2,v_3\right)$$

$\left(x,y,z\right)=\left(x_0,y_0,z_0\right)+\alpha \left(v_1,v_2,v_3\right),\alpha \in R$ Ecuación vectorial de la recta

Ejemplo

Hallar la ecuación vectorial de la recta que pasa por los puntos $M\left(3,2,1\right)$ y $S\left(–1,1,0\right)$.

Tenemos como datos dos puntos de la recta, entonces los vectores $\overrightarrow{MS}$ y $\overrightarrow{SM}$ son paralelos a dicha recta. Elegimos uno de ellos como vector director:

$$\vec{v}=\overrightarrow{MS}=\left(–4,–1,–1\right)$$

Podemos tomar cualquiera de los dos puntos dados cómo punto de paso, por ejemplo $M$. Entonces la ecuación es:

$$\left(x,y,z\right)=\left(3,2,1\right)+\alpha \left(–4,–1,–1\right),\alpha \in RecuaciónvectorialdelarectaMS$$

Para cada valor de $\alpha \in R,$se obtiene un punto de la recta. Por ejemplo, si $\alpha =–1$ se obtiene el punto $P_1\left(7,3,2\right)\in r.$

¿$\left(5,–3,1\right)\in r$?

Veamos si existe algún valor de $\alpha$ que verifique esta ecuación vectorial:

$$\left(5,–3,1\right)=\left(3,2,1\right)+\alpha \left(–4,–1,–1\right)$$

$$\{\begin{array}{c}3–4\alpha =5\\ 2–\alpha =–3\\ 1–\alpha =1\end{array}$$

Este sistema es incompatible, así que el punto no pertenece a la recta.

¿Para qué valor de $\alpha$ se obtiene el punto $S$?

Ecuaciones paramétricas de la recta

Hemos visto que la ecuación vectorial de una recta es:

$$\left(x,y,z\right)=\left(x_0,y_0,z_0\right)+\alpha \left(v_1,v_2,v_3\right)$$

Por igualdad de vectores:

$\{\begin{array}{c}x=x_0+\alpha v_1\\ y=y_0+\alpha v_2\\ z=z_0+\alpha v_3\end{array}$ $\alpha \in R$

Éstas son las ecuaciones cartesianas paramétricas de la recta.

Ecuaciones simétricas de la recta

Si $v_1,v_2,v_3$ son distintos de cero, entonces:

$$\alpha =\frac{x–x_o}{v_1},\alpha =\frac{y–y_o}{v_2},\alpha =\frac{z–z_o}{v_3}$$

Igualando, resulta:

$$\frac{x–x_o}{v_1}=\frac{y–y_o}{v_2}=\frac{z–z_o}{v_3}Ecuacionessimétricasdelarecta$$

Ejemplo

Consideremos la ecuación vectorial de la recta $MS$:

$$\left(x,y,z\right)=\left(3,2,1\right)+\alpha \left(–4,–1,–1\right),\alpha \in R$$

¿Cómo podemos obtener las ecuaciones paramétricas de la recta? Simplemente por igualdad de vectores escribimos:

$$\{\begin{array}{c}x=3–4\alpha \\ y=2–\alpha \\ z=1–\alpha \end{array}\alpha \in R,EcuacionesparamétricasdelarectaMS$$

Para obtener las ecuaciones simétricas, despejamos el parámetro e igualamos:

$$\alpha =\frac{x–3}{–4},\alpha =\frac{y–2}{–1},\alpha =\frac{z–1}{–1}$$

$$\frac{x–3}{4}=y–2=z–1,EcuacionessimétricasdelarectaMS$$

Recta definida como intersección de dos planos

Dos planos no paralelos ${\pi }_1:a_{1}x+b_{1}y+c_{1}z+d_1=0$ y ${\pi }_2:a_{2}x+b_{2}y+c_{2}z+d_2=0$ determinan al cortarse una recta en R3 que queda expresada por el sistema de ecuaciones lineales:

$$r:\{\begin{array}{c}{a}_{1}x+b_{1}y+c_{1}z+d_1=0\\ a_{2}x+b_{2}y+c_{2}z+d_2=0\end{array}$$

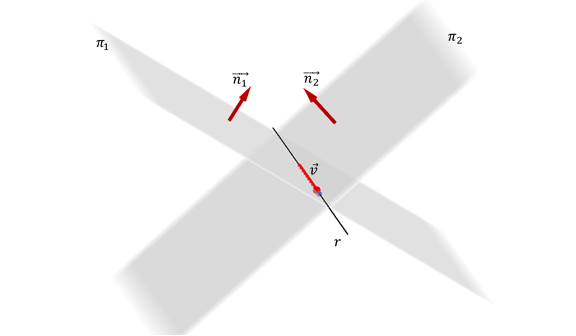
Ejemplo

Consideremos el siguiente ejemplo:

$$r:\{\begin{array}{c}x+y+z+1=0{\pi }_1\\ x–y–z+2=0{\pi }_2\end{array}$$

Éste es un sistema de $2x3$ (de 2 ecuaciones con 3 incógnitas) cuyo conjunto solución es la recta $r$.

¿Cómo podemos hallar un vector director de la recta y un punto de la misma?

Para obtener $\vec{v}$ , debe tenerse en cuenta que:

Por lo tanto $\overrightarrow{n_1}\times \overrightarrow{n_2}$ es un vector paralelo a $r$. Así encontramos un vector director de $r$:

$$\vec{v}=\overrightarrow{n_1}\times \overrightarrow{n_2}=\left(0,2,–2\right)$$

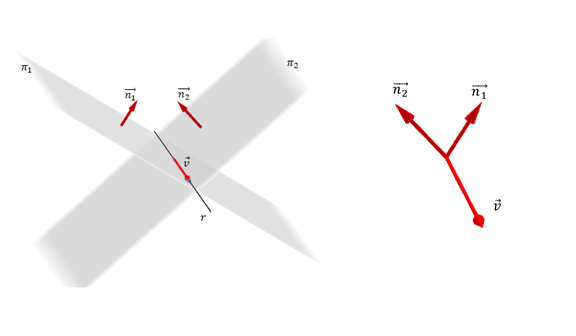
Para hallar un punto $P_0\in r$ , podemos fijar el valor de una de las variables en el sistema de ecuaciones que define a la recta, por ejemplo fijemos arbitrariamente $z=0$

Reemplazando en el sistema, nos queda:

$$\{\begin{array}{c}x+y+1=0\\ x–y+2=0\end{array}sistema2\times 2$$

Resolviendo este sistema, obtenemos: $x=–\frac{3}{2},y=\frac{1}{2}$ por lo cual un punto de la recta es $P_0\left(–\frac{3}{2},\frac{1}{2},0\right)$.

Con la información obtenida, estamos en condiciones de escribir la ecuación vectorial de la recta:

$$r:\left(x,y,z\right)=\left(–\frac{3}{2},\frac{1}{2},0\right)+\lambda \left(0,2,–2\right),\lambda \in R$$

Observación: Si para buscar un punto de la recta fijáramos $x=0$ (en lugar de $z=0$), nos quedaría el siguiente sistema: $\{\begin{array}{c}y+z+1=0\\ –y–z+2=0\end{array}$que es incompatible.

¿Por qué se produce esta incompatibilidad? Porque no hay ningún punto de la recta en el plano $x=0$, o sea la recta no interseca al plano $x=0$.

En resumen:

Dada una recta $r:\{\begin{array}{c}{a}_{1}x+b_{1}y+c_{1}z+d_1=0\\ a_{2}x+b_{2}y+c_{2}z+d_2=0\end{array}$

podemos obtener un vector director calculando el producto vectorial $\overrightarrow{n_1}\times \overrightarrow{n_2}$ .

Para obtener un punto de la recta, fijamos arbitrariamente el valor de una de las variables y resolvemos el sistema 2×2 resultante.

Ejemplo

Retomemos el ejemplo anterior:

$$r:\{\begin{array}{c}x+y+z+1=0{\pi }_1\\ x–y–z+2=0{\pi }_2\end{array}$$

Otra forma de obtener la ecuación vectorial de la recta es resolver el sistema de ecuaciones que la define.

Escribimos la matriz ampliada asociada al sistema:

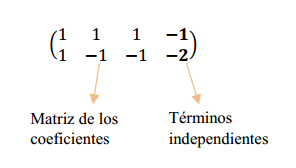
Aplicamos operaciones elementales entre filas para resolver el sistema de ecuaciones:

$$\left(\begin{array}{cccc}1& 1& 1& –1\\ 1& –1& –1& –2\end{array}\right)\underset{F_2\to F_2–F_1}{\to }\left(\begin{array}{cccc}1& 1& 1& –1\\ 0& –2& –2& –1\end{array}\right)$$

$$\underset{F_2\to –\frac{1}{2}{F}_2}{\to }\left(\begin{array}{cccc}1& 1& 1& –1\\ 0& 1& 1& 0,5\end{array}\right)\underset{F_1\to F_1–F_2}{\to }\left(\begin{array}{cccc}1& 0& 0& –1,5\\ 0& 1& 1& 0,5\end{array}\right)$$

$$\left(\begin{array}{cccc}1& 0& 0& –1,5\\ 0& 1& 1& 0,5\end{array}\right)$$

Y ahora escribimos el sistema simplificado:

$$\{\begin{array}{c}x=–1,5\\ y+z=0,5\end{array}$$

O sea:

$$\{\begin{array}{c}x=–1,5\\ y=0,5–z\end{array}$$

Entonces el conjunto solución se puede expresar así:

$$S=\left\{\left(x,y,z\right)\in R^3|x=–1,5\wedge y=0,5–z\right\}$$

Y podemos escribir la ecuación vectorial de la recta $r$:

$$\left(x,y,z\right)=\left(–1,5;0,5–z;z\right)$$

Llamando $z=\lambda$ , resulta:

$$r:\left(x,y,z\right)=\left(–1,5;0,5;0\right)+\lambda \left(0,–1,1\right),\lambda \in R$$