Deber: Lea, analice y subraye las ideas principales y secundarias en la Pág.: 174, además realice un mapa conceptual de la página expuesta en hojas de papel ministro, OBSERVAR Y ANALIZAR LOS EJERCICIOS RESUELTOS EN LAS PAGINAS PLANTEADAS.
La geometría analítica estudia las lineas y figuras geométricas mediante la aplicación de técnicas básicas de álgebra y análisis matemático en un determinado sistema de coordenadas.
En consecuencia, la geometría analítica es una rama de las matemáticas que analiza en detalle todos los datos de las figuras geométricas, es decir, el volumen, los ángulos, el área, los puntos de intersección, sus distancias, entre otros.
La característica fundamental de la geometría analítica es que permite la representación de las figuras geométricas a través de fórmulas.
Por ejemplo, las circunferencia son representadas por ecuaciones polinómicas de segundo grado mientras que las rectas son expresadas con ecuaciones polinómicas de primer grado.
La geometría analítica surge en el siglo XVII por la necesidad de dar respuestas a problemas que hasta el momento no tenían solución. Tuvo como máximos representantes a René Descartes y Pierre de Fermat.
En la actualidad muchos autores la señalan como una creación revolucionaria en la historia de las matemáticas, ya que representa el inicio de las matemáticas modernas.
Índice [Ocultar]
Historia de la geometría analítica
El término geometría analítica surge en Francia en el siglo XVII por la necesidad de dar respuestas a problemas que no podían resolverse usando el álgebra y la geometría de forma aislada, sino que la solución estaba en el uso combinado de ambas.
Principales representantes de la geometría analítica
Durante el siglo XVII dos franceses por casualidades de la vida realizaron investigaciones que de una forma u otra terminaron en la creación de la geometría analítica. Estas personas fueron Pierre de Fermat y René Descartes.
En la actualidad se considera que el creador de la geometría analítica fue René Descartes. Esto se debe a que publicó su libro antes que el de Fermat y también a la profundidad con la Descartes trata el tema de la geometría analítica.
Sin embargo, tanto Fermat como Descartes descubrieron que las lineas y la figuras geométricas podían ser expresadas mediante ecuaciones y la ecuaciones podían expresarse como lineas o figuras geométricas.
De acuerdo a los descubrimientos realizados por los dos se puede decir que ambos son los creadores de la geometría analítica.
Pierre de Fermat
Pierre de Fermat fue un matemático francés que nació en 1601 y murió en 1665. Durante su vida realizó estudios a la geometría de Euclides, de Apolonio y de Pappus, con el objeto de solventar los problemas de medición que existían para esa época.
Posteriormente estos estudios desencadenaron la creación de la geometría. Los mismos terminaron siendo expresados en su libro “Introducción a los lugares planos y sólidos” (Ad Locos Planos et Solidos Isagoge), que fue publicado 14 años después de su muerte en 1679.
Pierre de Fermat aplicó en 1623 la geometría analítica a los teoremas de Apolonio sobre los lugares geométricos. También fue quien aplicó por primera vez la geometría analítica al espacio de tres dimensiones.
René Descartes
También conocido como Cartesius fue un matemático, físico y filósofo que nació el 31 de marzo de 1596 en Francia y murió en el año 1650.
René Descartes publicó en 1637 su libro “Discurso sobre el método de conducir rectamente la razón y buscar la verdad en las ciencias” mejor conocido como “El Método” y desde allí se introdujo el término geometría analítica al mundo. Uno de sus apéndices era “La Geometría”.
Elementos fundamentales de la geometría analítica
La geometría analítica está conformada por los siguientes elementos:
El sistema de coordenadas cartesianas
Este sistema se denomina así en honor a René Descartes.
No fue él quien lo nombró, ni quien completó el sistema de coordenadas cartesianas, pero si fue quien habló de coordenadas con números positivos permitiendo que futuros estudiosos lo completaran.
Este sistema está compuesto por el sistema de coordenadas rectangulares y el sistema de coordenadas polares.
Sistemas de coordenadas rectangulares
Se le denomina sistemas de coordenadas rectangulares al plano formado por el trazo de dos rectas numéricas perpendiculares entre sí, donde el punto de corte coincide con el cero común.
Entonces este sistema quedaría conformado por una recta horizontal y otra vertical.
La recta horizontal es el eje de las X o el eje de las abscisas. La recta vertical sería el eje de las Y o el eje de las ordenadas.
Sistema de coordenadas polares
Este sistema se encarga de verificar la posición relativa de un punto en relación a una recta fija y a un punto fijo sobre la recta.
Ecuación cartesiana de la recta
Esta ecuación se obtiene de una recta cuando se conocen dos puntos por donde pasa la misma.
Linea recta
Es aquella que no se desvía y por lo tanto no tiene ni curvas ni ángulos.
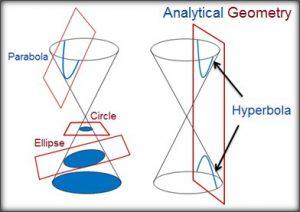
Cónicas
Son las curvas definidas por las rectas que pasan por un punto fijo y por los puntos de una curva.
La elipse, la circunferencia, la parábola y la hipérbola son curvas cónicas. A continuación se describen cada una de ellas.
Circunferencia
Se le denomina circunferencia a la curva plana cerrada que es formada por todos los puntos del plano que equidistan de un punto interior, es decir, del centro de la circunferencia.
Parábola
Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo (foco) y de una recta fija (directriz). Entonces, la directriz y el foco son los que definen la parábola.
La parábola puede ser obtenida como sección de una superficie cónica de revolución por un plano paralelo a una generatriz.
Elipse
Se denomina elipse a la curva cerrada que describe un punto al moverse en un plano de manera tal que la suma de sus distancias a dos (2) puntos fijos (llamados focos), es constante.
Hipérbola
Se denomina hipérbola a la curva definida como el lugar geométrico de los puntos del plano, para los cuales la diferencia entre las distancias de dos puntos fijos (focos) es constante.
La hipérbola tiene un eje de simetría que pasa por los focos, denominado eje focal. También tiene otro que es la mediatriz del segmento que tiene a los puntos fijos por extremos.
Aplicaciones
Existen variadas aplicaciones de la geometría analítica en distintos ámbitos de la vida diaria. Por ejemplo, podemos encontrar la parábola, uno de los elementos fundamentales de la geometría analítica, en muchas de las herramientas que se utilizan cotidianamente en la actualidad. Algunas de estas herramientas son las siguientes:
Antena parabólica
Las antenas parabólicas cuentan con un reflector generado como consecuencia de una parábola que gira sobre el eje de dicha antena. La superficie que se genera como resultado de esta acción lleva por nombre paraboloide.
Esta capacidad del paraboloide es denominada propiedad óptica o propiedad de reflexión de una parábola, y gracias a esta es posible que el paraboloide refleje las ondas electromagnéticas que recibe del mecanismo de alimentación que compone a la antena.
Puentes colgantes
Cuando una soga sostiene un peso que es homogéneo pero que, a la vez, es considerablemente mayor al peso de la propia soga, el resultado será una parábola.
Este principio es fundamental para la construcción de puentes colgantes, que suelen estar sostenidos por amplias estructuras de cables de acero.
El principio de la parábola en puentes colgantes ha sido utilizado en estructuras como el puente Golden Gate, ubicado en la ciudad de San Francisco, en Estados Unidos, o el Gran Puente del Estrecho de Akashi, que se encuentra en Japón y une la Isla de Awaji con Honshū, isla principal de ese país.
Análisis astronómico
La geometría analítica también ha tenido usos muy concretos y determinantes en el ámbito de la astronomía. En este caso, el elemento de la geometría analítica que toma protagonismo es la elipse; la ley del movimiento de los planetas de Johannes Kepler es reflejo de ello.
Kepler, matemático y astrónomo alemán, determinó que era la elipse la curva que se ajustaba mejor al movimiento de Marte; previamente había probado el modelo circular propuesto por Copérnico, pero en medio de sus experimentaciones, dedujo que la elipse servía para dibujar una órbita perfectamente similar a la del planeta que estudiaba.
Gracias a la elipse, Kepler pudo afirmar que los planetas se movían en órbitas elípticas; esta consideración fue el enunciado de la llamada segunda ley de Kepler.
A partir de este descubrimiento, enriquecido más adelante por el físico y matemático inglés Isaac Newton, fue posible estudiar los movimientos orbitacionales de los planetas, y aumentar el conocimiento que se tenía sobre el universo del que formamos parte.
Telescopio Cassegrain
El telescopio Cassegrain lleva su nombre en honor a su inventor, el físico de origen francés Laurent Cassegrain. En este telescopio se utilizan los principios de la geometría analítica porque está compuesto principalmente por dos espejos: el primero es de forma cóncava y parabólica, y el segundo se caracteriza por ser convexo e hiperbólico.
La ubicación y naturaleza de estos espejos permite que el defecto conocido como aberración esférica no tenga lugar; este defecto impide que los rayos de luz se reflejen en el foco de un lente determinado.
El telescopio Cassegrain es muy útil para la observación planetaria, además de ser bastante versátil y sencillo de manejar.
No hay comentarios:
Publicar un comentario